The main focus of my research up to now is developing stochastic models to understand the maintainace of diversity in biological systems. I start from modeling random mutants in a population with constant size in one speices to modeling the interactions of wild type and mutants under demographic fluctuations, and finally extend those approaches to model coevolution between two species in eco-evolutionary dynamic.
Mutant Games
We introduce a new model, named as mutant games. The interactions of a random mutant with resident types in a population are modeled by a dynamical payoff matrix. When a mutant appears, a new column and row are added in the payoff matrix. When one type goes extinct, the corresponding column and row are deleted.
Mutant games is based on a combined perspective of evolutionary game theory and population genetics. In many evolutionary game theoretical models, the number of types is usually fixed and payoff matrix is typically predefined. This can be a constraint to model a biological population, where mutations are often considered to be random. The concept that every mutant brings a new type in our model, is analogous to the infinite-alleles model in population genetics. The main difference is that the infinite-alleles model has mainly been considered under neutral or constant selection so far, but the mutant game is considered under frequency dependent selection (including constant selection as a speical case) and any selection intensity.
Many questions like fixation probabiity of a random mutant, the diversity and the average fitness changes under continuous random mutations, can be investigated based on the mutant games model (Huang et. al, JTB, 2010; Huang et. al, Nature Commmunications, 2012; Huang et. al, BMC Evolutionary Biology, 2012).
Stochastic game dynamics in populations with changing size
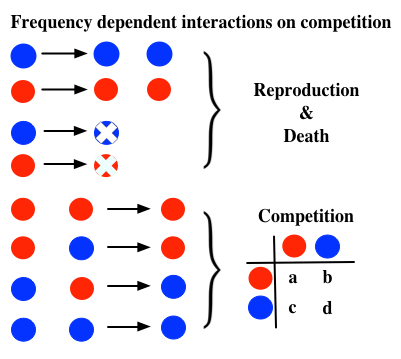
All natural populations are under demographic fluctuations, where the numbers of individuals in these populations change over time. While models assuming constant population size may be mathematically convenient, they are not necessary biologically relevant. we work on a model to capture the demographic fluctuations arising from ecological competitions between different types in a population. We use the format of chemical reactions to model different possible events in a population, like reproduction, death, and competitions. The aim of this work is to model frequency dependent interactions under stochastic demographic fluctuations and its impact on the population dynamics. We compare the dynamics with those from the classical game theoretical models without changing population size, like replicator dynamics, or from traditional ecological models without stochastic effects, like Lotka-Volterra equations. While our
model recovers the classical approaches in certain limits, e.g. large population sizes or assuming specific reaction rates, the outcome can differ compeletly in other cases where stochasiticity is not neglectale (Huang et. al, PNAS, 2015). Our model can be an useful alternative approach for ecologists using determintisc approaches to model inter- or intra- specific interactions. In the next step, we would like to extend the model to an evolutionary context, where mutations can happen besides of reproduction, death, and competitions (In preparation).
Prey predator coevolution
The concept of eco-evolutionary dynamics has been considered to be more and more important in the coevolution of prey and predator. Prey species can improve their defence capability, with a trade-off of decreased growth rates. In the meanwhile, predator species can also evolve to improve their predation ability, with a trade-off of decreased reproduction. Using those methods we developed in modeling random mutants and demographic fluctuations, we build a coevolutionary model to study the predator-prey dynamics. We are intersted in follwing questions: Does the prey evolve to use one best strategy or a diverse group of strategies in defence? (The same question could be referred to the predator.) How is diversity maintained in such a coevolutionary system? This is a joint project with Dr. Lutz Becks, the Community Dynamic group in Max Planck Institute for Evolutionary Biology (Huang, Traulsen, Werner, Becks, in preparation).
Species competition under limited resource
Multiple-resource competition models have been a leading theme that covers a broad spectrum of fields. The cornerstone of the issue is to understand how biological diversity depends on the amount and number of resources available in the ecosystem. This problem has been addressed by means of deterministic approaches that assume a priori number of species with non-evolving characteristics. In those approaches, oscillations and chaos are the main driving mechanisms sustaining the levels of diversity. However, real populations are finite such that under a scenario of strong oscillations species can easily reach extinction. Here, we address the multiple-resource competition in finite populations from an adaptive perspective, where species can evolve in their way of using resource. We use the monad equation R/(R+K) to define the growth of a species under a given resource, where R is the amount of resource available and K is the half-saturation representing its efficacy in using this resource. We consder K is an evolving parameter for different species with constrains, e.g. species can not evolove to use all kinds of resource effectively. We obersve more number of coexisting species than the number of resources if the selection is not too weak and species interactions are frequency dependent. This is a joint project with Prof. Paulo R. A. Campos in the Universidade Federal de Pernambuco (Huang, Ferreira, de Oliveria, Campos, submitted).
