Our research lies at the intersections of evolution with ecology and with medicine. Using mathematical models, we study which factors promote or hamper rapid adaptation to changing environments. Whether populations succeed in adapting to harsh environmental change or go extinct is one of the key questions of evolutionary biology. The answer is of relevance in very different contexts with opposite goals: in conservation biology (where we hope for adaptation and species persistence) and in medicine or agriculture (where we want to prevent successful adaptation, i.e. the evolution of resistance).
The adaptive process in these (and other) scenarios is often subject to strong stochasticity. Well-adapted genotypes are often initially rare, either because they were selected against in the previous environment and segregate only at low frequency in the population or because they appear de novo through mutation, recombination, horizontal gene transfer etc. Despite of having a selective advantage, they may therefore suffer stochastic loss instead of establish. Much of our work turns around this stochastic establishment process.
We mostly develop population genetics models but we also work on epidemiological models.
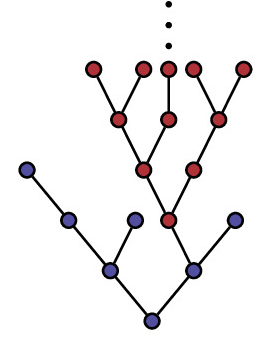One of the main tools in our research is provided by
branching process
theory.
Branching processes are a special class of stochastic processes
with a discrete state space. Their characteristic
property is that individuals reproduce independently from each
other. This relatively simple structure allows to treat many problems analytically.
We mainly use branching processes to determine the establishment probability of beneficial alleles
across a range of scenarios.
But we also apply them to derive accurate approximations for the passage times of beneficial alleles
(i.e. the times by which they reach a given frequency in the population) by accounting for stochasticity
in the early phase of spread. Branching processes with immigration can be used
to approximate the frequency of deleterious alleles in the standing genetic variation.
Uecker H., and Hermisson J. (2011) On the fixation process of a beneficial mutation in a variable environment. Genetics 188:915--930. (doi)
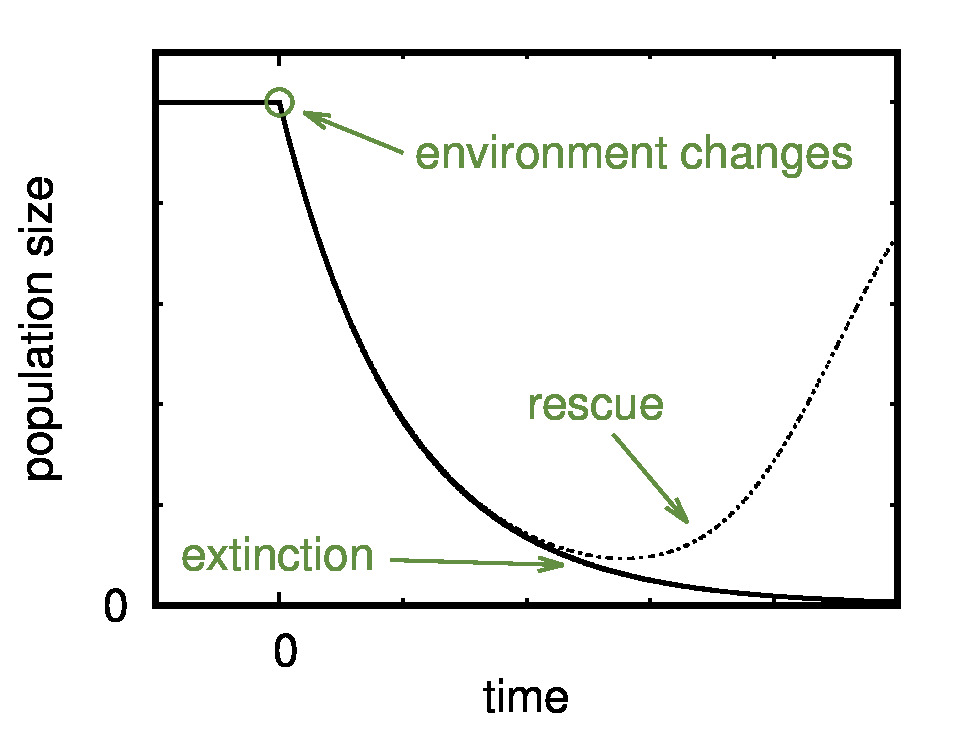A focus of our research is on models of evolutionary rescue, where
evolution and ecology are inherently intertwined. Environmental change,
if severe, can drive a population extinct unless the population succeeds
in adapting to the new conditions fast enough ("evolutionary rescue").
We investigate how genetic and environmental factors
such as recombination, selfing, population structure, or competition
among individuals influence the probability of population survival.
Czuppon P., Blanquart F., Uecker H.*, and Débarre F.* (in press) The effect of habitat choice on evolutionary rescue in subdivided populations. The American Naturalist. (doi)
Santer M. and Uecker H. (2020) Evolutionary rescue and drug resistance on multicopy plasmids. Genetics 215(3): 847-868.
(doi)
Uecker H. (2017)
Evolutionary rescue in randomly mating,
selfing, and clonal populations. Evolution 71: 845--858.
(doi)
Uecker H. and Hermisson J. (2016) The role of recombination in evolutionary rescue. Genetics 202:1--12.
(doi)
Uecker H., Otto S.P., and Hermisson J. (2014) Evolutionary rescue in structured populations. The American Naturalist 183:E17--E35.
(doi)
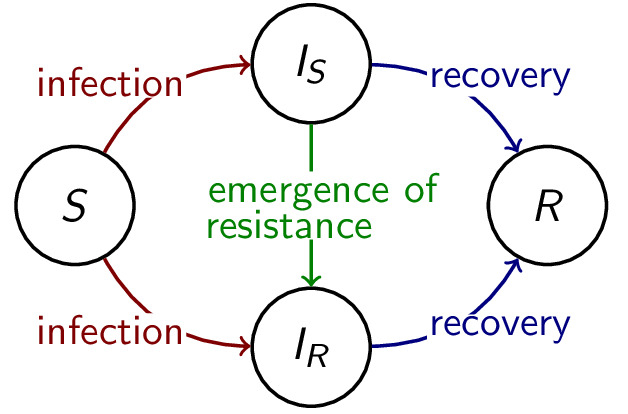
The evolution of antimicrobial resistance during treatment is
an instance of (undesired) evolutionary rescue.
Using within-host and between-host models and nested models, we study
how various treatment strategies such as combination therapy
or drug dosage influence the emergence and spread of resistance
to antibiotics and other antimicrobial drugs.
More recently, we have started to investigate the role of plasmids
in resistance evolution.
Uecker H. and Bonhoeffer S. (2021) Antibiotic treatment protocols
revisited: The challenges of a
conclusive assessment by mathematical modeling. Journal of the Royal Society Interface 18: 20210308. (doi)
Lagator M., Uecker H., and Neve P. (2021) Adaptation at different points along antibiotic concentration gradients.
Biology Letters 17: 20200913. (doi)
Santer M. and Uecker H. (2020) Evolutionary rescue and drug resistance on multicopy plasmids. Genetics 215(3): 847-868.
(doi)
Sciré J., Hozé N.*, and Uecker H.* (2019) Aggressive or moderate drug therapy for infectious diseases? Trade-offs between
different treatment goals at the individual and population levels. PLoS Computational Biology 15(8): e1007223.
(doi)
*equal contribution
Uecker H. (2018) Effectively evolution-proof antibiotics? Trends in Microbiology 26(12): 969-970.
(doi)
Uecker H. and Bonhoeffer S. (2017) Modeling antimicrobial
cycling and mixing: Differences arising from an individual-based versus
a population-based perspective. Mathematical Biosciences 294: 85--91.
(doi)
Tepekule B., Uecker H., Derungs I., Frenoy A., Bonhoeffer S. (2017)
Modeling antibiotic treatment in hospitals: A systematic approach shows
benefits of combination therapy over cycling, mixing, and mono-drug therapies.
PLoS Computational Biology 13(9): e1005745.
(doi)
Through hybridization and backcrossing, advantageous alleles can cross species barriers, a process termed "adaptive gene introgression". However, the beneficial allele may be linked to alleles that are deleterious in the new genetic background or in the habitat of the sister species. These linked deleterious can be lost through recombination but some may hitchhike to fixation. We determined the probability of adaptive gene introgression in the presence of linked deleterious alleles and hitchhiking probability of these alleles.
Uecker H., Setter D., and Hermisson J. (2015) Adaptive gene introgression after secondary contact. Journal of Mathematical Biology 70:1523--1580. (doi)